一、形态学操作
- 形态学,即数学形态学(Mathematical Morphology),是图像处理过程中一个非常重要的研究方向。形态学主要从图像内提取分量信息,该分量信息通常对于表达和描绘图像的形状具有重要意义,通常是图像理解时所使用的最本质的形状特征。例如,在识别手写数字时,能够通过形态学运算得到其骨架信息,在具体识别时,仅针对其骨架进行运算即可。形态学处理在视 觉检测、文字识别、医学图像处理、图像压缩编码等领域都有非常重要的应用。
- 形态学操作主要包含:腐蚀、膨胀、开运算、闭运算、形态学梯度(Morphological Gradient) 运算、顶帽运算(礼帽运算)、黑帽运算等操作。腐蚀操作和膨胀操作是形态学运算的基础,将腐蚀和膨胀操作进行结合,就可以实现开运算、闭运算、形态学梯度运算、顶帽运算、黑帽运算、击中击不中等不同形式的运算。
1. 连通性
1.1 邻接
- 连通性
- 是描述区域和边界的重要概念
- 必要条件:
- 两个像素的位置是否相邻
- 两个像素的灰度值是否满足特定的相似性准则(或者是否相等
- 邻接分类:
- 4邻接:
- 像素p(x,y)的4邻域是:(x+1,y);(x-1,y);(x,y+1);(x,y-1),用N4(p)表示像素p的4邻接
- D邻接:
- 像素p(x,y)的D邻域是:对角上的点 (x+1,y+1);(x+1,y-1);(x-1,y+1);(x-1,y-1),用ND(p)表示像素p的D邻域
- 8邻接:
- 像素p(x,y)的8邻域是: 4邻域的点 + D邻域的点,用N8 (p)表示像素p的8邻域
- 4邻接:

1.2 连通性
- 根据连通性的定义,有4联通、8联通和m联通三种。
- 4联通:
- 对于具有值V 的像素p和q,如果q在集合N4(p)中,则称这两个像素是4连通。
- 8联通:
- 对于具有值V 的像素p和q,如果q在集合N8(p)中,则称这两个像素是8连通。
- m联通:
- 对于具有值V的像素p和q,p、q满足m联通的条件:
- q在集合N4(p)中,或 q在集合ND(p)中,
- 并且N4(p)与N4(q)的交集为空(没有值V的像素) 则称这两个像素是m连通的,即4连通和D连通的混合连通。
- 对于具有值V的像素p和q,p、q满足m联通的条件:



2. 形态学操作
2.1 腐蚀和膨胀
- 腐蚀:
- 它能够将图像的边界点消除,使图像沿着边界向内收缩,也可以将小于指定结构体元素的部分去除。
- 用一个结构元素扫描图像中的每一个像素,用结构元素中的每一个像素与其覆盖的像素做“与”操作,如果都为1,则该像素为1,否则为0。

- 膨胀:
- 膨胀操作将与当前对象(前景)接触到的背景点合并到当前对象内,从而实现将图像的边界点向外扩张。如果图像内两个对象的距离较近,那么在膨胀的过程 中,两个对象可能会连通在一起。膨胀操作对填补图像分割后图像内所存在的空白相当有帮助。
- 用一个结构元素扫描图像中的每一个像素,用结构元素中的每一个像素与其覆盖的像素做“与”操作,如果都为0,则该像素为0,否则为1。


import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread("./image/image3.png")
# 2 创建核结构
kernel = np.ones((5, 5), np.uint8)
# 3 图像腐蚀和膨胀
erosion = cv.erode(img, kernel) # 腐蚀
dilate = cv.dilate(img,kernel) # 膨胀
# 4 图像展示
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(img)
axes[0].set_title("原图")
axes[1].imshow(erosion)
axes[1].set_title("腐蚀后结果")
axes[2].imshow(dilate)
axes[2].set_title("膨胀后结果")
plt.show()
2.2 开闭运算
- 开运算和闭运算是将腐蚀和膨胀按照一定的次序进行处理。
- 但这两者并不是可逆的,即先开后闭并不能得到原来的图像。
- 开运算(开——>最后一步是膨胀)
- 开运算是先腐蚀后膨胀,
- 其作用是:
- 分离物体,消除小区域,消除毛刺。
- 特点:
- 消除噪点,去除小的干扰块,而不影响原来的图像

- 闭运算(闭——>最后一步是腐蚀)
- 闭运算与开运算相反,是先膨胀后腐蚀,
- 作用是
- 消除/“闭合”物体里面的孔洞,
- 特点:
- 可以填充闭合区域。

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img1 = cv.imread("./image/image5.png")
img2 = cv.imread("./image/image6.png")
# 2 创建核结构
kernel = np.ones((10, 10), np.uint8)
# 3 图像的开闭运算
cvOpen = cv.morphologyEx(img1,cv.MORPH_OPEN,kernel) # 开运算
cvClose = cv.morphologyEx(img2,cv.MORPH_CLOSE,kernel) # 闭运算
# 4 图像展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img1)
axes[0,0].set_title("原图")
axes[0,1].imshow(cvOpen)
axes[0,1].set_title("开运算结果")
axes[1,0].imshow(img2)
axes[1,0].set_title("原图")
axes[1,1].imshow(cvClose)
axes[1,1].set_title("闭运算结果")
plt.show()

2.3 礼帽和黑帽
- 礼帽运算
- 原图像与“开运算“的结果图之差
- 用来分离比邻近点亮一些的斑块
- 得到外部毛刺信息
- 黑帽运算
- 为”闭运算“的结果图与原图像之差
- 用来分离比邻近点暗一些的斑块
- 得到内部躁点信息
import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img1 = cv.imread("./image/image5.png")
img2 = cv.imread("./image/image6.png")
# 2 创建核结构
kernel = np.ones((10, 10), np.uint8)
# 3 图像的礼帽和黑帽运算
cvOpen = cv.morphologyEx(img1,cv.MORPH_TOPHAT,kernel) # 礼帽运算
cvClose = cv.morphologyEx(img2,cv.MORPH_BLACKHAT,kernel)# 黑帽运算
# 4 图像显示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img1)
axes[0,0].set_title("原图")
axes[0,1].imshow(cvOpen)
axes[0,1].set_title("礼帽运算结果")
axes[1,0].imshow(img2)
axes[1,0].set_title("原图")
axes[1,1].imshow(cvClose)
axes[1,1].set_title("黑帽运算结果")
plt.show()
二、图像平滑
1. 图像噪声
- 椒盐噪声
- 也称为脉冲噪声,是图像中经常见到的一种噪声,它是一种随机出现的白点或者黑点

- 高斯噪声
- 是指噪声密度函数服从高斯分布的一类噪声

2. 图像平滑简介
2.1 卷积操作动态展示
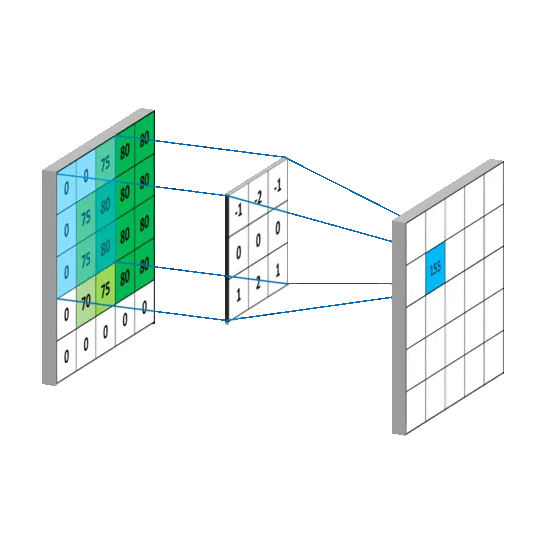
2.2 均值滤波
- 采用均值滤波模板对图像噪声进行滤除

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 均值滤波
blur = cv.blur(img,(5,5))
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([]) plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('均值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.3 高斯滤波
- 利用二维高斯是去除高斯噪声
- 离像素点越远的点,对该像素点的权值贡献越小

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogGasuss.jpeg')
# 2 高斯滤波
blur = cv.GaussianBlur(img,(3,3),1)
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('高斯滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
2.4 中值滤波
- 用像素点邻域灰度值的中值来代替该像素点的灰度值
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 中值滤波
blur = cv.medianBlur(img,5)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('中值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
三、直方图
1. 灰度直方图
- 直方图是图像中像素强度分布的图形表达方式。
- 它统计了每一个强度值所具有的像素个数。
- 不同的图像的直方图可能是相同的
- 掩膜:
- 创建蒙版,透过mask进行传递,可获取感兴趣区域的直方图
- 掩膜在遥感影像处理中使用较多,当提取道路或者河流,或者房屋时,通过一个掩膜矩阵来对图像进行像素过滤,然后将我们需要的地物或者标志突出显示出来。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2 统计灰度图
histr = cv.calcHist([img],[0],None,[256],[0,256])
# 3 绘制灰度图
plt.figure(figsize=(10,6),dpi=100) plt.plot(histr)
plt.grid()
plt.show()
## 掩膜操作
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1. 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2. 创建蒙版
mask = np.zeros(img.shape[:2], np.uint8) mask[400:650, 200:500] = 255
# 3.掩模
masked_img = cv.bitwise_and(img = img,mask = mask)
# 4. 统计掩膜后图像的灰度图
mask_histr = cv.calcHist([img],[0],mask,[256],[1,256])
# 5. 图像展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img,cmap=plt.cm.gray)
axes[0,0].set_title("原图")
axes[0,1].imshow(mask,cmap=plt.cm.gray)
axes[0,1].set_title("蒙版数据")
axes[1,0].imshow(masked_img,cmap=plt.cm.gray)
axes[1,0].set_title("掩膜后数据")
axes[1,1].plot(mask_histr)
axes[1,1].grid()
axes[1,1].set_title("灰度直方图")
plt.show()
2. 直方图均衡化
- 直方图均衡化
- 增强图像对比度的一种方法
- cv.equalizeHist(): 输入是灰度图像,输出是直方图均衡图像

- 自适应的直方图均衡
- 将整幅图像分成很多小块,然后再对每一个小块分别进行直方图均衡化,最后进行拼接

## 直方图均衡化
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1. 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2. 均衡化处理
dst = cv.equalizeHist(img)
# 3. 结果展示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img,cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[1].imshow(dst,cmap=plt.cm.gray)
axes[1].set_title("均衡化后结果")
plt.show()

## 自适应的直方图均衡
import numpy as np
import cv2 as cv
# 1. 以灰度图形式读取图像
img = cv.imread('./image/cat.jpeg',0)
# 2. 创建一个自适应均衡化的对象,并应用于图像
clahe = cv.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
# 3. 图像展示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img,cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[1].imshow(cl1,cmap=plt.cm.gray)
axes[1].set_title("自适应均衡化后的结果")
plt.show()

四、边缘检测
1. 边缘检测的原理
- 基于搜索:
- 通过寻找图像一阶导数中的最大值来检测边界,然后利用计算结果估计边缘的局部方向,通常采用梯度的方向,并利用此方向 找到局部梯度模的最大值,代表算法是Sobel算子和Scharr算子。

- 基于零穿越:
- 通过寻找图像二阶导数零穿越来寻找边界,代表算法是Laplacian算子。

2. Sobel算子


import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 计算Sobel卷积结果
x = cv.Sobel(img, cv.CV_16S, 1, 0)
y = cv.Sobel(img, cv.CV_16S, 0, 1)
# 3 将数据进行转换
Scale_absX = cv.convertScaleAbs(x) # convert 转换 scale 缩放
Scale_absY = cv.convertScaleAbs(y)
# 4 结果合成
result = cv.addWeighted(Scale_absX, 0.5, Scale_absY, 0.5, 0)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100) plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(result,cmap = plt.cm.gray),plt.title('Sobel滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()
## 将上述代码中计算sobel算子的部分中将ksize设为-1,就是利用Scharr进行边缘检测
x = cv.Sobel(img, cv.CV_16S, 1, 0, ksize = -1)
y = cv.Sobel(img, cv.CV_16S, 0, 1, ksize = -1)

3. Laplacian算子


import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 laplacian转换
result = cv.Laplacian(img,cv.CV_16S)
Scale_abs = cv.convertScaleAbs(result)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(Scale_abs,cmap = plt.cm.gray),plt.title('Laplacian检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()

4. Canny算法
- Canny边缘检测算法是由4步构成,分别介绍如下:
- 第一步:噪声去除
- 使用高斯滤波器去除噪声
- 第二步:计算图像梯度
- 第三步:非极大值抑制
- 第四步:滞后阈值

- 第一步:噪声去除
- 判断是否为边界点的两个条件:
- 是否大于最大边界阈值,如果大于,则是边界点;
- 如果小雨最小值,直接舍弃
- 如果小于最大阈值,大于最小阈值,则看当前点是否与其他边界点相连,如果相连则是边界点;
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/horse.jpg',0)
# 2 Canny边缘检测
lowThreshold = 0
max_lowThreshold = 100
canny = cv.Canny(img, lowThreshold, max_lowThreshold)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(canny,cmap = plt.cm.gray),plt.title('Canny检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()
5. 其他算子

